University entrance examinations. Industrial Technology
This test is designed to answer FOUR of the following six questions. Each exercise is worth 2.5 points. If you answer more than one exercise, only the first four will be assessed.
As this is not an official exam, you can do the whole test and it will not affect the final mark.
Previous considerations of the test.
- Exercise 1: when the answers are checked it is shown whether the answer is correct or incorrect (green if it is correct and red if it is not).
- In all the other exercises, the incorrect answer is followed by a display showing the correct answer and, in most cases, the steps to follow to get there.
- As an extra, I have added a help to the user in the sections I thought necessary. This is an automatic calculation that may help you to understand the calculations done.
- Plus, there is a step by step solution in some cases (in which the algerbra is not that clear to express by words) through JavaScript using MathJax.
Plus, there is an HTML coded calculator, in case you need to do some calculations.
Exercise 1
Indicate the correct answer to each question. If you do not indicate the answers, the questions will be considered unanswered.
[In each question you can only choose ONE answer. Question well answered: 0.5 points; question incorrectly answered: -0.16 points; question not answered: 0 points.]Question 1
A mountain hut wants to install photovoltaic panels to provide a maximum consumption during the winter of 150 kWh per month. Determine the surface area of the panels required assuming a radiation density of 700 W/m2 during the winter months, a solar gain of 4 hours a day for 30 days a month and an efficiency of the installation of 8%.
Question 2
A person on a skateboard goes down a 30m long slope with a slope of 5°. He starts from the rest and does not take the brake at any time. The mass of the person and the skateboard is 82 kg. How fast will the skate go at the end of the descent if all the losses are neglected?
Question 3
If you have a 12 H7/g6 adjustment, the tolerance of the hole is (180) µm and the tolerance g6 of the shaft is (-6-17) µm, thus it can be stated that:
Question 4
The Ti-6Al-4V titanium alloy is used in the manufacture of malleable prostheses. It contains 4.5% vanadium (V), 6.5% aluminium (Al) and the rest is titanium (Ti). In obtaining this alloy, how much aluminium is needed to combine it with 20 kg of titanium?
Question 5
A university residence wants to reduce its annual electricity consumption, which currently stands at 41 MWh. To do this, it wants to replace the lighting with low-consumption lighting and use presence detectors in common areas. It is estimated that the saving in electricity consumption will be 12 %. If the company indicates that its electricity mix is 360 g of CO2/(kWh), how much annual CO2 emissions savings will the residence achieve?
Exercise 2
The aim is to design the circuit that controls a fire alarm. The alarm must be triggered when the fire alarm goes off, or when two or more of these three conditions are met: a temperature limit has been exceeded, there is smoke in the room, and/or the temperature has risen sharply. Answer the following questions using the following status variables:
| alarm: \begin{align} a=\begin{cases}1: active \\ 0: not active \end{cases}; \end{align} | push button: \begin{align} p=\begin{cases}1: pressed \\ 0: not pressed \end{cases}; \end{align} | smoke: \begin{align} f=\begin{cases}1: detected \\ 0: not detected \end{cases}; \end{align} | temperature: \begin{align} t=\begin{cases}1: if&t\geqq 58ºC \\ 0: if&t\lt 58ºC\end{cases}; \end{align} | temperature increment: \begin{align} t=\begin{cases}1: if&t\geqq 8ºC/min \\ 0: if&t\lt 8ºC/min\end{cases}; \end{align} |
Exercise 3
The following table shows the values recorded in a tensile test with a test piece of length L0 = 125mm and diameter d=8mm.
| Deformation ε | 0 | 1·10-3 | 2·10-3 | 3·10-3 | 4·10-3 | 0,02 | 0,05 | 0,1 |
|---|---|---|---|---|---|---|---|---|
| Tension σ [MPa] | 0 | 69 | 138 | 207 | 276 | 300 | 290 | 257 |
Exercise 4
The firefighters use a fire-fighting fan that eliminates smoke and removes large volumes of air. The fan blades have a diameter of d = 420 mm and the air is blown out at a rate of q = 33660 m3/h. The fan is driven by a four-cycle motor of power Pmot = 3,58kW rotating at n =3600 min-1. The fuel is diesel with a calorific value pc= 44,8 MJ/kg and density ρgasoil = 0,85 kg/L, and the engine has a consumption c = 1,4 L/h. The diesel emissions factor is FE = 2,87 kg CO2/L. Determine:
Exercise 5
The figure shows a folding garage door of length 2L. To open and close it, its highest point P is guided horizontally, to which a force F is applied. The centre of inertia of the door is at its midpoint and the vertical displacement of this point is forced by a guide. All friction is considered negligible.
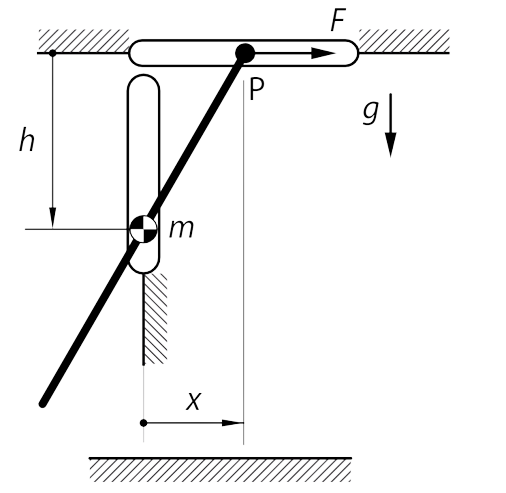
The door is held in repose in a generic position x. Determine, as a function of x:
Exercise 6
The municipal public lighting system of a town consists of n=308 light points, which are on, on average, t = 11 hours a day. Each light point uses a high pressure sodium vapour pump (VSAP) with a power of 100W. The tariff set by the electricity company sets an electricity cost of celectr = 0,1370 €/(kWh). In addition, the City Council has to assume an annual cost associated with the maintenance of this system cmant= 14,000 €.
Determine:
The city council wants to replace all the lighting points with new ones that will use LED technology bulbs with a power of Pled = 36W. Each light has a unit cost of €500 (including the bulb). The cost of the installation of the new lighting is estimated at cinst = 43,000€. In this installation the maintenance cost can be neglected. Determine: